Recursion is a programming strategy used for breaking complex computation problems into small sub-problems that can be solved. The recursion problem is self-referential. The strategy is deployed when a function makes copies of itself to solve sub-problems of a computation. Every recursive function has a base case that allows the recursion to end peacefully.

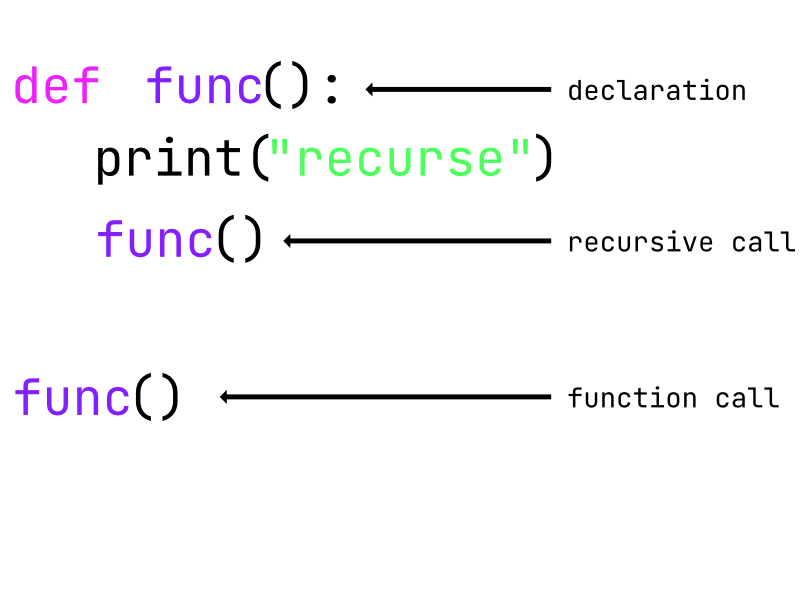
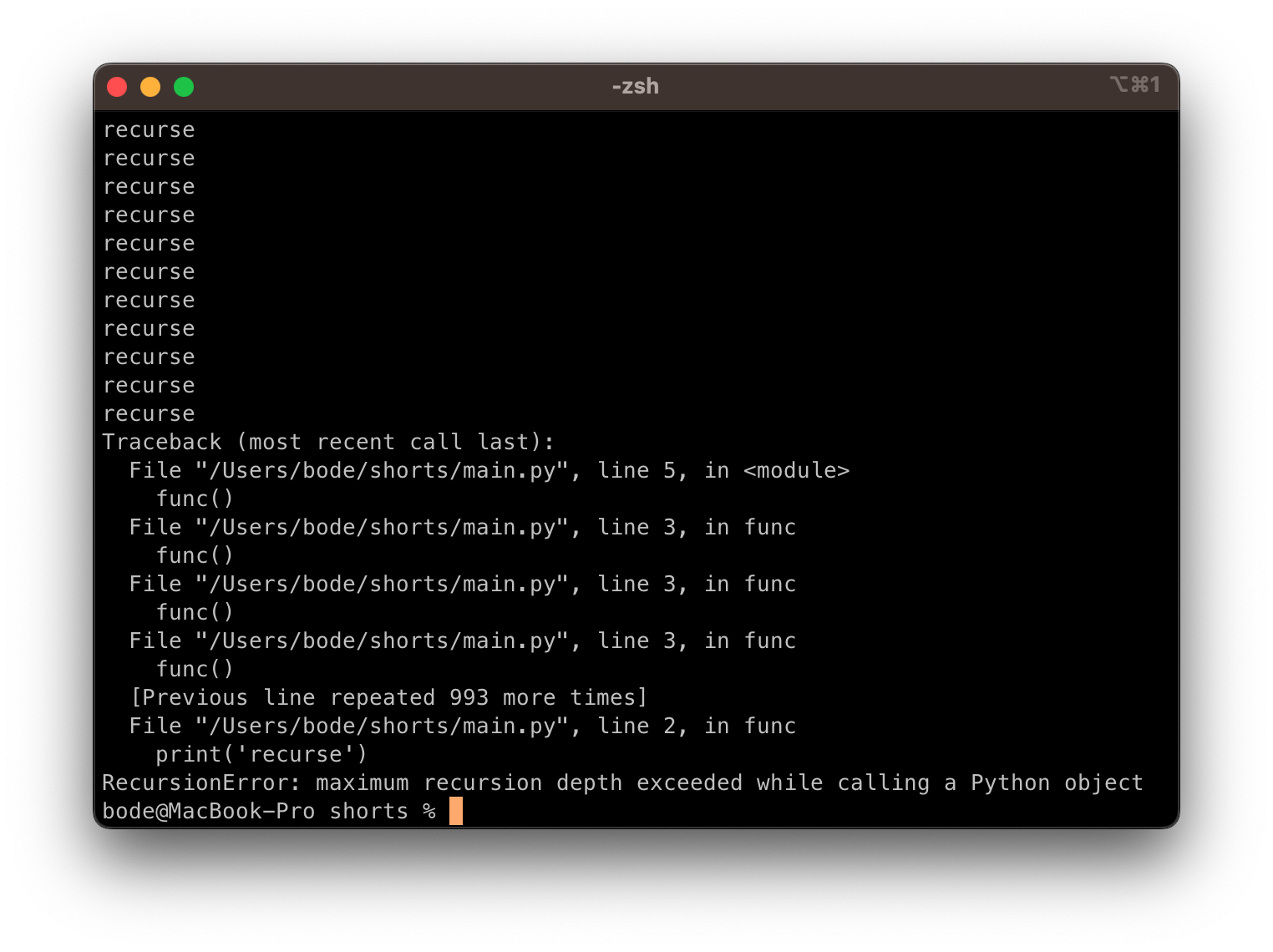
The recursive call will keep creating copies of func() which consequently will keep printing "recurse" for eternity 😀, no am just kidding till your computer runs out of memory. But python has a maximum recursion dept that the recursion call will be terminated once the threshold has been reached.

You can get the limit using the sys module's getrecursionlimit() function.

import sys
sys.getrecursionlimit() # 1000

If the default recursion limit is not good enough for you, you can increase it using the setrecursionlimit()

sys.setrecursionlimit(2000)

It is recommended that you do not temper with the recursion limit as the default is more than enough for most of your use cases

How to Exit A Recursion

To exit a recursion you must specify a base case that once met the recursion will end.

def func(n=0):
  if n == 5: return # base case
  print('recurse')
  func(n + 1)

We are using the positional argument n=0 to track the recursion calls, once the base case, n == 5 has been met, the function will return. Note that the base condition will not be met if you don't increment n by 1 in the recursive call. The recursion will only print 'recurse' five times because of the base case.

Using Recursion In Python

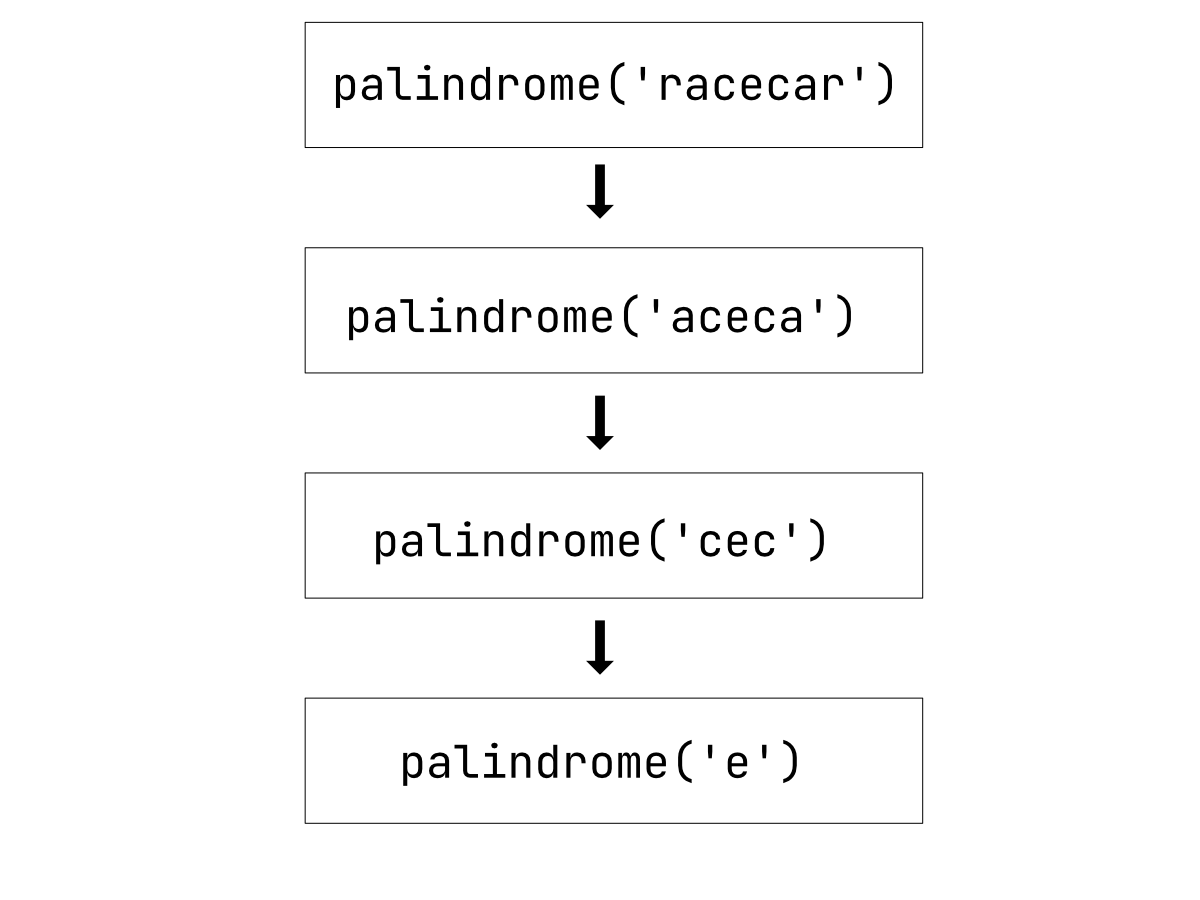
Let's check if a word is a palindrome. A palindrome is a word that reads the same backward, for example, racecar.

def palindrome(word):
    last_index = len(word) - 1
    if len(word) <= 1: # base case
        return True
    if word[0] != word[last_index]: # base case
        return False
    return palindrome(word[1:last_index])
palindrome('racecar') # True

We have two base cases for when the word is a palindrome and when it is not. The recursion works by removing the first and last characters and then checking if the current first and last characters are the same until there is only one character, then the function will return True or if the characters don't match it will return False.

Another common recursion problem is factorial. A factorial is the product of all numbers less than or equal to the given number.

We can use recursion to solve for the factorial of any given number in python.

def factorial(n):
  if n == 0:
    return 1
  return n * factorial(n - 1)

factorial(4) # 24

the number n will be multiplied by its referenced self until the base condition has been reached n == 0

 ### Recursion vs. Iteration Almost any recursive problem can be solved iteratively but recursions are generally simpler and more concise. The trade-off for simple recursive functions is that they consume more memory as the computer keeps track of all the copies of the function created.